“A language that doesn't affect the way you think about programming, is not worth knowing.”-Alan Perlis
APL is an ancient language, in many ways different than most programming languages today. The goal of this document is to give a basic introduction for those who would like to understand or use the language, while still providing a taste of the language to those who would like to skim.
Here's a sample of old style APL to give you an idea what it looks like (you can come back and understand it later; it's a fairly complex way of calculating
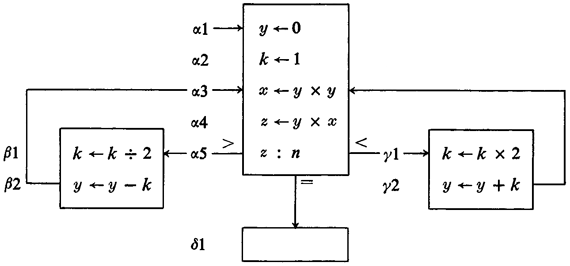
It is useful to evaluate languages by dividing their enhancements into three different categories:
The syntax of APL is wild and entertaining, and the structure is simple. It is based in a mathematical way of thinking: equations are preferred over sequences of steps to be performed. For example, in the programming style, a summation can be written with a for loop; or it can be represented with a ∑. Two different ways of writing the same thing, and APL prefers the latter. Because of the density of ideas to characters, APL can put you in the “flow.” It can also be a pain to decipher.
APL is based on arrays (a vector based language). That may seem rather specialized, but Excel is basically a GUI system for arrays. A lot of the things people now do in Excel used to be done in APL. Would Excel be better if it had been built solidly on a framework like APL, instead of being an ad-hoc GUI with visual basic smooshed in? (The answer is yes). Databases can also be thought of as a set of vectors, and APL was used for data analysis before SQL even existed.
Ken Iverson started creating APL as part of his thesis, and later published a book, called A Programming Language. That is where we will start our journey. It wasn't even meant as a language for computers, it was meant for humans to read and write, and thus allowed structure that you couldn't have on a teletype. Here is an example that performs a matrix multiply:
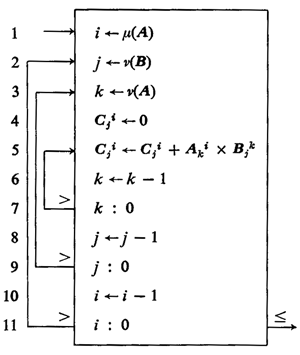
Look at the branches and loops: they are drawn lines, instead of using braces or other structures. Notice that the indices for the matrixes are written as subscripts and superscripts, just like a human would on paper. Computers from the 1960s couldn't reasonably do these things, but if the language were invented today, we could.
The : sign was used to represent an if statement, or a comparison. On each line leading from the if statement, there is a comparator, indicating to follow that arrow if the left side of the : compared with the right side is true. It should be asked, is this the best way to structure code? To really answer that, one would need to spend a lot of time trying it (IDA Pro uses a similar method to display disassembled code, and I think it's really nice, but maybe it wouldn't be useful everywhere).
Three types of branches, behold the three.


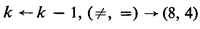
One of the most important operations of this early APL was the / sign, which used binary to select items from an array, or columns from a matrix. If it was a one, that column was selected, if it was a zero, that column wasn't. So, for example, look at these examples for a bit and see if you can figure out how it works:
| 1 0 1 1 / 1 2 3 4 | would return 1 3 4. |
| 1 1 1 0 0 / X | would return the first three columns of X, and |
| 0 0 1 1 / 10 11 12 13 | would return 12 13. |
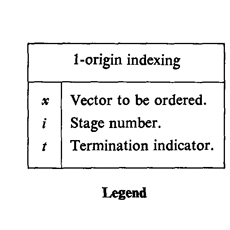
Cheat sheet (I would give you one, but yours is more powerful). If you're going to learn APL, take notes! There's no way you can remember all these symbols the first time. If you come across a symbol you can't remember, write it down like I did here in this list:
| ← | Assignment. x ← 5 sets x to five |
| v(x) | Number of rows in x |
| u(x) | Number of columns in x |
| ⍺ | An array starting with ones, thus ⍺3 is 1 1 1 0 0 0... |
| ⍵ | An array starting with zeros, thus ⍵2 is 0 0 1 1 1 1... |
| p(x) | The physical address of x |
Bubble sort. You now have enough experience in the 1962 version of APL to understand this bubble sort if you want to:
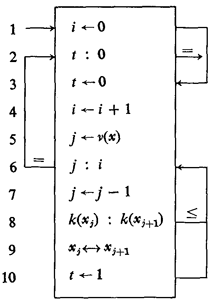
You might be interested to know that old APL was later used to describe machine architectures. For example, RAM can be thought of as a binary M×36 matrix (yes, some early computers had 36 bits at each memory address, it wasn't until later that 8 bits became the norm), and an accumulator (register) is just a 38 bit vector.
But.....eventually IBM decided they had to make APL work on a computer. They wrote a book called APL: The Language and Its Uses. IBM had good documentation back in the day. Reading it might remind you of the old DOS computer manuals, even the smell. But I will summarize the main points of the language for you, you can use it today.
Here's an example of the old style, and the same expression written in the new style, optimized for teletypes. For example, instead of writing:
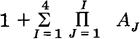
Let's quickly look through some of the characters of new APL, because they are funny and entertaining. They are now part of unicode, but you might need to map them to your keyboard.
| ⍝ | comment symbol |
| ⍋ | sort ascending |
| ⍒ | sort descending |
| ⌽ | rotate around vertical axis |
| ⊖ | rotate around horizontal axis |
| ⍟ | logarithm |
| ∆ | up triangle is actually a normal char |
| ⌹ | matrix divide |
| ¨ | do to each matrix in a list |
| ∘. | do each parameter to each matrix in list |
| | | remainder |
| ⍳ | quickly generate an array of integers |
| ⌈ | ????? mystery ?????? |
| ⌊ | ????? mystery ?????? |
Understanding documentation is important, and here is where you can practice. Visit the official APL documentation at IBM. Look for the document titled “Language Reference” then figure out what the ⌈ character does. Next look for the ⌊ character. Did you guess correctly?
In the new version of APL, × was used for multiplication, and * raises to a power (that is, 2*4 = 16). The ÷ symbol is used for division, not / like in a lot of languages. You need to use a special ¯ character for negative numbers. Writing X52 was no longer possible, you needed to write X[5 ; 2]. The brackets are powerful, you can select multiple elements as in X[1 2 3 4 5], and even select the same column multiple times, as in X[;1 3 1 3 1].
If you want to use APL practically, a common symbol is the shape symbol: ⍴. It takes a list of numbers and shapes it into a one, two, three, or N-dimensional matrix. The values before ⍴ indicate the number in each dimension, and the values after ⍴ indicate the data to be used in the shape. If there are not enough values after, then they will be repeated until the dimensions are filled. See what you can learn from these examples and the results.
⍝ generate a two dimensional array
3 3 ⍴ ¯9
¯9 ¯9 ¯9
¯9 ¯9 ¯9
¯9 ¯9 ¯9
⍝ generate a one dimensional array
7 ⍴ 1 0
1 0 1 0 1 0 1
⍝ an array of characters
2 4 ⍴ ,'ab'
a b a b
a b a b
⍝ (the , makes it a vector.
⍝ Sometimes , concatenates)
You can store that in a variable using ← for example: X ← 3 4 ⍴ 1 2 3 4 stores a three dimensional array in X. You can print the result just by typing X on a line by itself:
X
1 2 3 4
1 2 3 4
1 2 3 4
Operators work on vectors as easily as on individual elements. 1 + 1 yields 2, but if you have multiple columns, each gets added to its partner. So 1 2 + 1 2 yields 2 4. If there is a single element on one side, and a vector on the other, then the single element gets applied to every element on the other. Example:
2 4 6 ÷ 2gives the answer
1 2 3
Combinations: the +/ combination adds all the elements of a vector, and the ×/ combination multiplies all the elements of a vector.
Here are some commands that are useful for selecting from a matrix or vector, or otherwise rearranging:
| ↑ | select the first N columns from vector V. |
| ↑ | If N is negative, select the last N columns. |
| ↑ | When selecting from a matrix, specify both dimensions. |
| ↑ | Example: 3 ¯4 ↑ M |
| , | Join two matrixes M1 , M2 |
| ,[n] | Join along the nth dimension |
| ,[n] | Many operators can use this dimension marker |
| +[n] | Example: 1 0 1 0 +[1] 4 4 ⍴ 1 0 |
| ↓ | Drop columns from a matrix. |
| ↓ | ¯3 ↓ V drops the last three columns of V. |
The creator of APL had a mathematical background, so he was familiar with the idea that everything can be a function. In fact, a language can be considered entirely made of syntactic sugar on functions. For example, consider the expression 3 * 5 + 2. In many programming languages, it could be written add(mult(3, 5), 2). On the command line, you could write it with the pipe: echo 3 | mult 5 | add 2 (with proper executables having been defined).
APL functions are defined using the ∇ sign. Each function can have no more than one parameter on the left, and one parameter on the right. This seems like a limitation at first, but since each parameter can have as many dimensions as you want, it's not really a problem.
∇ f1 param1 ⍝ This is an example of ⍝ a function with one ⍝ parameter. Fill in code ∇
∇ param1 f2 param2 ⍝ this is an example of ⍝ a function with two ⍝ parameters. It does nothing ∇
∇ rv ← param1 f3 param2 ⍝ this is an example of ⍝ a function with a ⍝ return value. This ⍝ function always returns 2 ⍝ note the next line rv ← 2 ∇
A lot of built-in functions have monadic and diadic functions, that is, if you call them with one parameter, they do something different than if you call them with two parameters.
| ÷ | invert, 1/x |
| ⌽ | reverse vector |
| | | absolute value |
| ⌹ | invert matrix |
| ⍴ | size of the parameter |
Quick self-test: look back and see what the absolute value symbol | does when it has two parameters. It's not always absolute value.
APL uses goto. If you don't know how to write good code with goto statements, Knuth taught how to do it. Some programmers still don't like it, which is good because it forces them to use fewer loops. Some programmers still don't like it, and they create their own control structures. APL lets you do that with the execute symbol. Here are some examples for examination and understanding.
⍝ This is an an infinite loop. ⍝ The → means 'jump to the label "start" start: ⎕ ← 'To infinity and beyond!' → start ⍝ Try to guess what the ⎕ means.
⍝ This is an example 'if' statement.
⍝ When the expression is true, the
⍝ jump happens. When it's {empty set},
⍝ it continues to the next line.
⍝ There are as many types of 'IF' as
⍝ there are ways to generate {empty set}
→ (x = 5) ⍴ label
'skip when x is five'
label:
'always execute this line'
⍝ We define a function that will
⍝ emulate a more natural 'IF' statement.
⍝ The ⍎ symbol executes a statement in
⍝ quotes. The ~ symbol is logical not.
∇rv← body IF condition
→ (~condition) ⍴ out
rv ← ⍎body
out:
∇
⍝ How to use the new 'IF' function:
⍝ The body has to go in quotation marks
⍝ The condition does not
'3 + ¯2 + 7' IF 7 ≠ 5
To print Hello World, type ⎕ ← 'Hello World'. To get input, just put the box in the equation where you want the input to go. For example, if you want the user to to give you values for x and y in the equation 5x + 4y + 2 then you can just replace x and y: 5⎕ + 4⎕ + 2. APL will prompt the user to fill in the blanks.
I heard about APL from my grandpa, who told me it could be used to write programs much more concisely than other languages (my grandpa then told me how bad he had it in his day, with his ancient slow 10 baud modem.[1] Maybe he was exaggerating). APL is also worth learning because it gives you a chance to look into the mind of its creator, a man who spent many years fine-tuning his language to be as useful as possible.
Now you're ready for this introduction to an APL IDE, or to install the GNU APL environment, or even to understand this Conway's Game of Life solver.
To learn the language, it's fun to start solving problems. Once you've downloaded an APL environment, here are some good ones to get you started:
It also says, “There is a great temptation for a user who has just learned about ⍳ to try an expression like ⍳1000 on the terminal to see what happens. The typing speed of a terminal is approximately 15 characters per second. After watching the first 100 numbers or so type out, the user usually deplores his action and wants a way to stop the seemingly endless display.”

